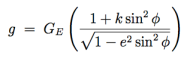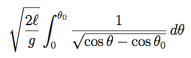Extreme Musical Venues

No, I don’t mean this: www.extrememusic.com. But now that I’ve got your attention, I want to return to a topic I wrote about last month: the Earth’s gravity and its effect on mechanical metronomes (or, more abstractly, its effect on pendulums). That post boiled down this fact:

Pendulums near the poles will swing more quickly than pendulums of the same length near the equator.

Of course, that begs the question—how much more quickly? At the time of my previous post, I hadn’t researched the mathematics required to do this. But now I’ve crunched some numbers and have some results to share. Before that, though, let me set up some of the basic ideas behind the calculations.

1. The Earth isn’t a sphere. We know today that the Earth is an oblate spheroid, and is flatter at the poles than at the equator. The verification of this fact dates back to the 1730s, and is credited to Pierre Louis Maupertuis. It’s worth mentioning that the oblateness follows from Newton’s mechanics, of which Maupertuis was a notable advocate. [Maupertuis did many other things, and you can read about them in this book.]

2. Gravity varies according to latitude. This follows quickly from point (1) above, though the first attempt at a precise formula was made by Alexis Claude de Clairaut in his 1743 treatise, Théorie de la figure de la terre. W. W. R. Ball has a short summary of Clairaut’s work. Today, we use a more precise formula, as part of the World Geodetic System:

Here, G_E ≈ 9.78033 is gravity at the equator, e ≈ 0.0818192 is the Earth’s eccentricity (which measures the “sphereness” of the ellipsoid, ranging from  0 to 1), and k ≈ 0.00193185 is a parameter that depends on gravity at the poles. (Details can be found here on page 4-2). 

3. Pendulum formula requires calculus. I’m going to skip the derivation, and point you to Wikipedia on this one (grain of salt and all that). Here’s the formula for one “swoop” of a pendulum:

with l being the length of the pendulum and θ₀ being its initial angle.

4. Gravity decreases with altitude. The experts use something called the free-air correction to compensate for this. For example, Reynolds’ An Introduction to Applied and Environmental Geophysics states that the proper way to adjust the formula in part (2) above is by subtracting (3.086×10^-7)h, where h is your elevation above sea level (I’ve converted the units from Reynolds’ version).

Now we’re ready for some results! For all calculations, I took θ₀ = π/4, and l ≈ 0.229060. This way, a pendulum at sea level at the equator will beat exactly 120 times per minute. Then, I picked five extreme points on the surface of the Earth:  the summits of Chimborazo and Everest, and the Antarctic stations McMurdo, Russkaya, and Amundsen-Scott. And here’s what we have:

Location	Elevation	Latitude	Beats per Minute
Reference Point	0 m.	0°	120
Chimborazo	6268 m.	1.469° S	119.881
Everest	8848 m.	27.988° N	119.902
Russkaya	0 m.	74.766° S	120.296
McMurdo	0 m.	77.850° S	120.304
Amundsen-Scott	2835 m.	90° S	120.264

I’ve ignored the fact that the mass of the terrain that you’re standing on will affect the gravity at its summit (the Bouguer anomaly)—so the values for Everest and Chimborazo are probably a bit off. But, taking the numbers at their word, our hypothetical metronome will move the most quickly at McMurdo Station—which has the double-benefit of being both close to the pole (and thus closer to the center of the Earth) and having a low elevation. (In fact, McMurdo has the world’s southernmost port; you can go see what they’re up to right now.)

To conclude, it appears that a piece of music set to 120 beats per minute, that takes 5 minutes to perform, will finish almost exactly 1 beat sooner at McMurdo station than it would at the summit of Mount Everest. Not enough to mess anything up musically, but enough to notice. Extreme, right? (Not extreme enough for you? Then go read this comic.)

Beethoven in the Antarctic

If you’ve ever spent time learning to play a musical instrument, you’ve undoubtedly used a metronome—depending on your age, it may have looked something like this:

(For clarity, we’ll call that little trapezoid-shaped thingie the bob, while the bottom of the rod will be the pivot point.) The design of the mechanical metronome has not differed much since Johann Maelzel received this patent in 1815—more on this in a later post.

While today’s metronomes are often electronic devices, for centuries they were based on Galileo’s pendulum principle: the time taken by one full swing of a pendulum depends only on the bob’s distance from the pivot point (and on gravity). Crucially, the time is not dependent on the mass of the bob, or the width of the swing.* In fact, one early definition of the meter was the length of a pendulum that would swing from one end to the other in the space of two seconds.

In the end, though, this definition was rejected in favor of the so-called meridional definition: the distance along a meridian of the Earth from the Equator to the North Pole. Why the change? Well, it turns out the Earth isn’t a perfect sphere—it’s an oblate spheroid (that’s math-speak for “the spin of the Earth makes it bulge outward at the Equator”). So, the force of gravity is somewhat less strong at the poles than it is at the Equator.

Now back to the history of the metronome: musicians began to adopt the metronome in their compositions; Ludwig van Beethoven was notably one of the first to do so. By the 20th century, metronome notations (given in beats per minute) were included in nearly all musical works.

Given what we know about the Earth’s gravity, you may have already noticed that there’s a minor problem with metronomes—those at polar latitudes will click at a faster rate than those at equatorial latitudes. (Swiss Scientist & Mathematician Leonhard Euler gives a good summary of the issue in his 1738 work Von der Gestalt der Erden. See pages 4-5 of Langton’s translation, available here.)

Here’s the musical takeaway: if you are playing a piece that sets a tempo of 120 beats per minute, and are using a mechanical metronome to keep time, then you will play this piece more quickly at the South Pole than you would at the Equator. I do hope there are some musicians at the Amundsen-Scott Station who are enjoying the naturally-accelerated tempos of the region!

* I know what you’re thinking: it’s not actually this simple (it rarely is). There are some other factors in play, including the ever-menacing friction. But it’s close enough to the truth.